New Insights into Brain Flexibility and Stability
Novel mathematical model addresses a longstanding dilemma in neuroscience and possibly other fields
August 5, 2022
By Mario Aguilera
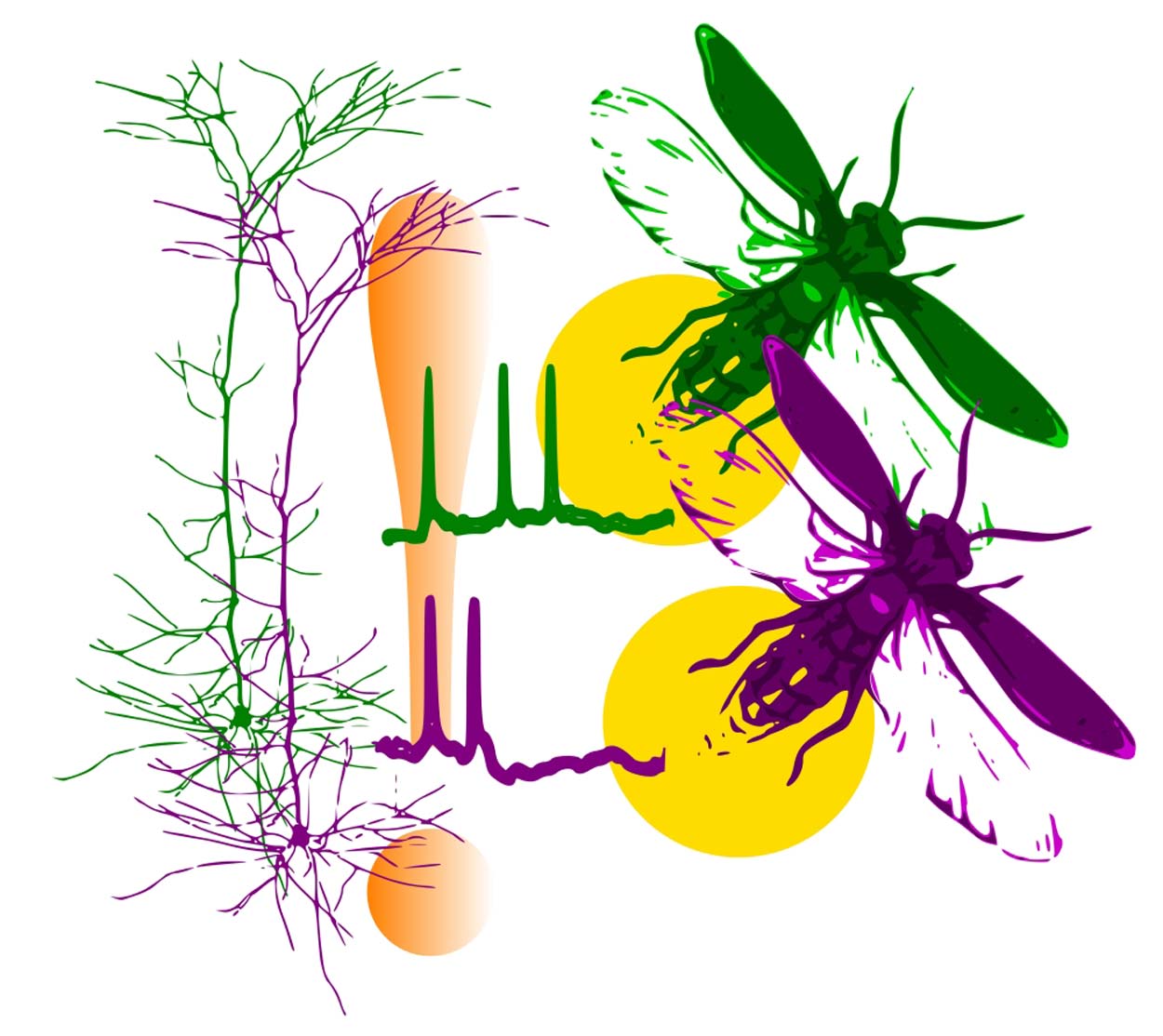
UC San Diego scientists developed a new mathematical model to understand properties of coincident activity of interacting agents. They applied the theory to understand how synchronous neuronal activity (left) changes connections between neurons, which leads to learning. Future applications of the theory could explain emergence of synchronized flashing in firefly swarms (right).
Aljadeff Lab, UC San Diego
Our brains are incredibly nimble, allowing us to form new memories throughout life, yet stable enough to retrieve precious memories from long ago. How can we do both? How is it that new memories do not erase old ones?
Addressing this long-standing quandary in neuroscience, University of California San Diego researchers have developed a new way of modeling basic neurobiological interactions. Department of Physics graduate student Bin Wang and School of Biological Sciences Assistant Professor Johnatan Aljadeff have developed a new theoretical tool to understand how frequently we expect connections between neurons in our brain to change. These changes, referred to as synaptic plasticity, are the biological implementation of learning, and occur when the two connected neurons emit spikes in synchrony. The new results, published in the journal Physical Review Letters, provide a new way of understanding what the "rules of synaptic plasticity" mean for the entire network, and the behaviors our brains produce.
The theory developed by Wang and Aljadeff predicts the strength of connections between neurons by accurately accounting for the rate and amplitude of coincident spikes of the two neurons.
"The special properties of coincidences revealed in the study help us understand how neuronal networks can acquire new memories when we go about our day on one hand, and remain stable without erasing everything that happened to us the day before on the other hand," said Aljadeff, a faculty member in the Department of Neurobiology. "If we know how active two connected neurons are, then we can compute how frequently there will be a coincidence between two neurons and how strong it will be."
The mathematical work on so-called "multiplicative shot-noise" was developed with neural networks in mind, but could be relevant in a range of other fields and natural phenomena. Swarms of fireflies, with individual fireflies flashing at random intervals, provide another relevant example. Coincident flashes of two fireflies may affect the strength of the interaction between the fireflies and the chance of them flashing together in the future. Wang and Aljadeff's new formula could help researchers decipher the synchronization and periodic nature of flashes of firefly swarms, a classical problem at the intersection of ecology, math and physics.
Other possible applications include environmental challenges as a result of climate change. In ecosystems where drought and habitat loss coincide, for example, the multiplicative process analyzed in this paper could help predict how such a coincidence could amplify damage to the environment.
"There are studies that show that big declines in ecological communities happen when there are coincident environmental stresses," said Aljadeff.
The paper marks the first research published by Aljadeff's laboratory, established at UC San Diego in 2020.
Also noteworthy is that Wang, who is an international student at UC San Diego, was able to complete the project despite difficulties due to travel and visa restrictions, along with pandemic impacts.
The research was supported by a Department of Energy grant (DE-SC0022042); the researchers also thank the UC San Diego Friends of the International Center for its support.
