Study Sheds Light on What Causes Cells to Divide
December 30, 2014
By Kim McDonald
When a rapidly-growing cell divides into two smaller cells, what triggers the split? Is it the size the growing cell eventually reaches? Or is the real trigger the time period over which the cell keeps growing ever larger?
A novel study published online today in the journal Current Biology has finally provided an answer to this long unsolved conundrum. And it's not what many biologists expected.
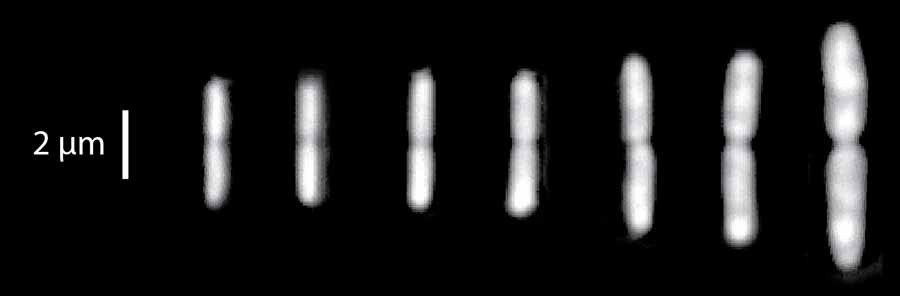
Dividing E. coli cells at seven different growth conditions. The faster they grow, the bigger they are.
Sattar Taheri-Araghi, UC San Diego
"How cells control their size and maintain stable size distributions is one of the most fundamental, unsolved problems in biology," said Suckjoon Jun, an assistant professor of physics and molecular biology at UC San Diego, who headed the research study with Massimo Vergassola, a professor of physics. "Even for the bacterium E. coli, arguably the most extensively studied organism to date, no one has been able to answer this question."
Finding a solution was more than a basic-science pursuit for the scientists, who pointed out that learning more about the triggers of cell division would enable researchers to better understand such processes as the runaway cell division that leads to cancer. To conduct the study, Jun and his colleagues developed a tiny device to isolate and physically manipulate individual genetic materials.
"It turned out that we can use this device to also follow the life history of thousands of individual bacterial cells for hundreds of generations," he said. "We looked at the growth patterns of the cells very, very carefully, and realized that there is something really special about the way the cells control their size."
"In our study, we monitored the growth and division of hundreds of thousands of two kinds of bacterial cells, E. coli and B. subtilis, under a wide range of tightly controlled steady-state growth conditions," said Jun. "This produced statistical samples about three orders of magnitude, or a thousand times better, than those previously available. We could thus pursue an unprecedented level of quantitative analysis."
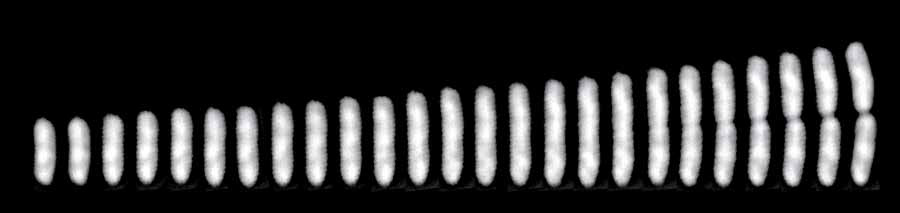
A time series of a single E. coli cell from birth to division.
The scientists found through their development of mathematical models that matched their experimental data that the growth of cells followed the growth law, essentially exponential growth based on a constant rate. But they also found to their surprise that cell size or the time between cell divisions had little to do with when the cells divided. Instead, to keep the distribution of different sized cells within a population constant, the cells followed what the researchers termed "an extraordinarily simple quantitative principle of cell-size control."
"Specifically, we showed that cells sense neither space nor time, but add constant size irrespective of their birth size," said Jun. "This ‘adder' principle automatically ensures stability of size distributions."
" E. coli and B. subtilis are one billion years divergent in evolution, and they are the textbook examples of the diversity of molecular details for biological controls in different bacterial species. Thus, their sharing the same quantitative principle for size maintenance is a textbook level discovery."
The two primary authors of the study were Sattar Taher-Araghi of UC San Diego and Serena Bradde of the City University of New York. In addition to Jun and Vergassola, other co-authors are John T. Sauls of UC San Diego, Norbert S. Hill of UC Berkeley, Petra A. Levin of Washington University and Johan Paulsson of the Harvard Medical School.
Jun's research effort was supported by a $240,000 grant from the Pew Charitable Trusts and a $1.6 million award from the Paul G. Allen Family Foundation, established by one of the co-founders of Microsoft. He also received a $1.15 million grant from the National Science Foundation to apply, together with his graduate students, the work from their research on cell division to annual "boot camps" that will educate San Diego-area high school and college students about an emerging field at the intersection of physics and biology called "quantitative biology"—in which the mathematical models of physics are used to simulate biological phenomenon. This mathematically based, quantitative biology approach was used to solve the problem of what prompts cells to divide.
"Quantitative biology is more than adding numbers to what biologists already know," explained Jun. "The power of the approach is to bring quantitative rigor from physical sciences to identify and solve important and interesting problems in biology."
